Summer (northern hemisphere) is now over. Meaning that the core of the music festival season has pretty much finished. If you attended any festival over the summer, I am sure that you had a schedule of bands or talks to see across the days. This schedule of yours, is just a subset of the schedule that was developed for the music festival itself. The bigger the festival becomes, the more difficult this scheduling is. Here is some ideas on what could occur when developing a music festival schedule.
One thing to note, this blog is simply about how I think one could use optimisation for music festivals, not the current practice.
Setting the scene
Let’s consider a single day of a music festival. The main thing to think about here is that there are numerous bands that will be playing across the course of the day. Also, there are multiple stages that the bands will be playing on. For some examples, I have used the website Clashfinder and collected some of the bigger festivals that occur in Germany, the UK and the US. Some examples are the Reeperbahn Festival, Glastonbury, Lattitude, Reading and Lollapalooza. Please take the time to look at a couple of these and think about the optimisation problems that you may see.
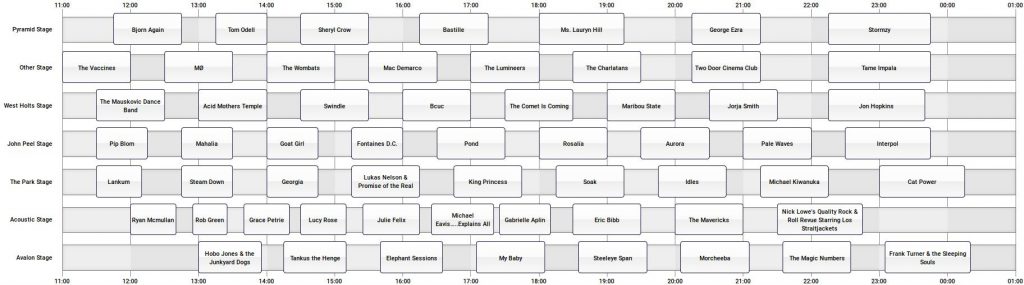
Potential optimisation problems
My first thought when looking at the music festival schedules was: Wow, there are a lot of cool acts that I want to see. Then I proceeded to use Clashfinder to work out which acts I could actually see.
The second thing was: This looks a lot like the solution to a parallel machine scheduling problem. Each of the stages are the machines, and the band sets are the jobs. Now, it is not exactly like a machine scheduling problem. The main reasons why not are because the following are fixed:
- The machine (stage) that the job (band) will be performed on.
- The order of the jobs (bands) on a machine (stage).
- The end time of all jobs (bands).
While it is not a parallel machine scheduling problem, there is still an optimisation problem that exists in developing this schedule.
Bring in Clashfinder
The reason that Clashfinder exists is that the scheduling of bands on the stages introduces clashes with other bands that you may want to see. Because the number of bands could be quite large, such as for Glastonbury, and there are large distances between the stages, again Glastonbury is a good example, then it can be difficult to see two bands that are on at similar times, even if there is only a small overlap. So the optimisation problem that one could consider in developing the schedule is to pick start times such that there is the smallest amount of overlap between stages.
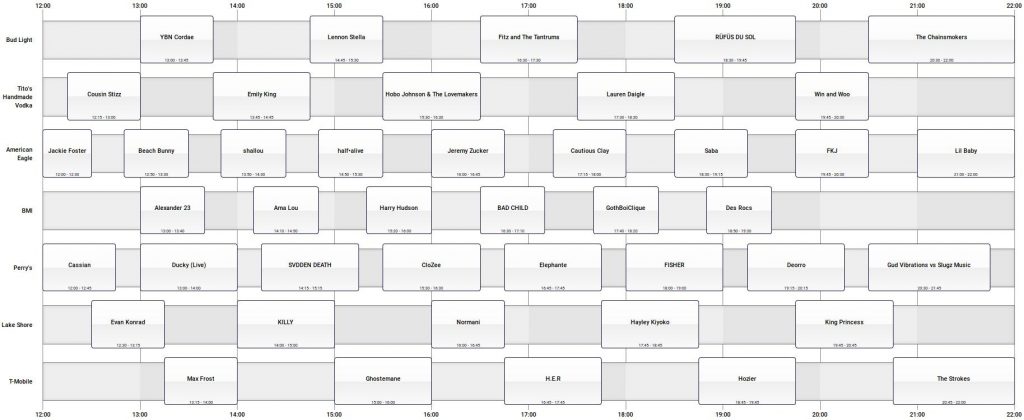
One of the best examples for avoiding clashes is for the Tito’s and Bud Light stages at Lollapalooza (see above). The band sets on these two stages are completely disjoint. Now, looking at the festival map, you can see that these two stages are very close, suggesting the need to schedule the band sets in this way. This introduces yet another aspect into the music festival scheduling problem.
Set time optimisation
I will first present an idea about how you could optimise the set times of the festival, and then follow up with some extensions to this model.
Decision variables
Lets assume that all of the decisions presented above are fixed. For example, the assignment of bands to stages, the order of the bands and the end time of the day. Then we have the following decisions:
- The start time of each set.
- The duration of each set.
Restrictions/constraints
A couple of restrictions, or constraints, need to be considered
- A minimum break time between the sets,
- A minimum set time (this could change throughout the day and be different per stage),
- A maximum set time (same as above, different with respect to time of day and stage),
- Typically, later bands have a longer set time than earlier bands, so this should be imposed.
There could also be a maximum break time. However, this is likely to be implied by the other constraints and the minimum and maximum set times.
Objective functions
There is not too much to consider in this problem. Making decisions about the start time and set duration that satisfy the constraints could be made fairly easily using a heuristic. The main difficulty arises with the objective function. In this case, I suggest the objective function of
- Minimise the total overlap of sets
This can be achieved by breaking the day up into 5 minute intervals and counting the number of concurrent sets in each interval. The aim of this objective is reduce the number of sets that are running at the same time. An alternative could to
- Minimise the unallocated set time, i.e. times that no band is playing
This alternative objective would result in a very similar schedule as the first one proposed. However, there is not a focus on the number of clashes.
The objectives are described in a linear setting, i.e. counting the number of clashes in each time interval. Consider these two scenarios with two time intervals:
- 4 overlapping sets in one interval and none in the other,
- each time interval has 2 overlapping sets.
Both have a cost of 4, while the former could be seen as worse than the latter. This could be avoided by modelling the objective as a quadratic function. So, in the former case the cost would be 16 and the latter case the cost would be 8.
Extensions to the optimisation model
There is one glaring issue with the above optimisation model. It assumes that all festival goers want to see all of the bands. However, everyone has different preferences, so there could be a lot less clashes than the first model assumes. Thus, we could look at a more intelligent way to optimise the set times.
This extension relies on expert knowledge of the bands and the fans that they attract. If it were possible to categories bands into groups that would have similar fan bases, then we could develop an optimisation model to avoid clashes for the different groups of fans. Let’s broadly categorise bands into 4 groups: rock, metal, punk and dance. We then assume that each fan will only want to avoid clashes for bands within the one category. Our objective then becomes:
- Minimise the total overlap of sets for each band category.
Again, quadratic terms could be used for this objective to avoid large amounts of overlap.
This new objective forms an optimisation model that is superior to the previous one. Mainly, clashes between bands who are in the rock and dance categories are no longer considered in the objective function. Thus, we are minimising the clashes for the bands that are most important to each group of fans.
Final extension
Festival sites can be very big places. If you would like to get between two different stages, it would be ideal if there was sufficient time between sets. This is easily integrated into our model by including a buffer time between sets of the same category. This buffer should be as large as the walking time between stages.
Consider two rock bands, All for Rock and Rock it Out, playing on Stages A and B respectively. It is not enough to just consider the set time of All for Rock and Rock it Out when assessing the clashes, but it has to be extended to account for the walking time between stages A and B.
Prepare for next summer
I liked the idea of using optimisation to adjust the set times for avoiding clashes. In reality, there may not be much scope for change, since all available time has been taken up. However, if there were some options, then the use of this simple optimisation model can help make the right decisions.

