Throughout many parts of the world food banks are operated by charities to help those experiencing food poverty. After collecting goods from companies and individuals, food bank organisations distribute those good throughout a network in order to satisfy demand to the best of their ability. In the UK, there are more than 2,000 food banks operating with the largest number being operated by the Trussel Trust. There are two typical structures for food banks, a warehouse model and the full distribution model. In the warehouse model, the food bank organisation does not directly hand out food, but provide food to charities. The second model involves a complex network of suppliers, warehouses and distribution centres. It is the full distribution that we will look at in this blog post.
Food bank organisation operate over a distribution network to transfer good from suppliers to those experiencing food poverty. If you have read any of my previous blogs, the idea of a network and distribution should highlight the possibility of an optimisation problem. Below we will discuss optimisation problems regularly encountered by food bank organisations.
Food rescue and distribution: a vehicle routing problem
The operations by food rescue organisations are very similar to courier, delivery and transportation organisations. For which there is a rich operations research literature. In order to solve the optimisation problems for food banks, it is possible to draw upon the methods developed for distribution and delivery organisations.
The delivery problem
First we focus just on the distribution side of the operation. The task for the food rescue organisation is to distribute goods from one or more centralised warehouses to the “front-line” distribution centres. Such a problem could be considered a variant of the vehicle routing problem. In the food rescue context, the centralised warehouse is the depot for the vehicles and goods and the “front-line” distribution centres are the customers.
The objective of the vehicle routing problem is find a set of routes for the available vehicles such that the goods are delivered to all customers at a minimum cost. The most important constraints are: i) every customer must be visited by exactly one vehicle and ii) all vehicle routes must start and end at the depot. Since you typically have more than one vehicle, then you will find a route for each vehicle that will be operated on that day. As an example, the warehouse is point 0 in the below image and all of the distribution centres (customers) are the coloured nodes. Each colour represents a different vehicle route.
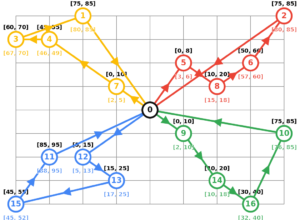
Source: Google
There are a number of complicating factors that make the VRP for food rescue organisations more challenging compared to the classical logistics setting, which include
- Heterogeneous set of goods to be distributed around the food bank network
- Limited availability of vehicles
- Limited opening times of receiving locations (typically because these are operated by volunteers)
- Limited funds to operate the vehicles, warehouses and distribution centres
Fortunately, these are complications that are easily modelled. Typically, it is possible to draw upon the literature from delivery and courier logistics to build a representative model.
The pickup and delivery problem
The VRP literature has a variant called the pickup and delivery problem. This extends the above problem where the vehicles pickup goods in addition to delivering them to customers. In the food rescue context, these two processes could be seen as disjoint. This is because the pickup locations are typically supermarkets or commercial kitchens and the delivery locations are the distribution centres. However, there are contexts where you may want to bypass the warehouse. For example, highly perishable goods may need to be delivered directly to the distribution centre from the supplier. In such contexts, the pickup and delivery problem could be more appropriate.
While this variant of the VRP is more complicated, there has been much research on the topic. As such, there are many algorithms available to solve such problems.
Uncertainty in food bank operations
A complicating aspect in optimisation problems for food banks is the uncertainty in operations. Some areas of uncertainty are:
- The supply of food
- The demand at each of the distribution centres
- The type of goods supplied and needed
- The availability of staff
- The availability of vehicles
This uncertainty makes the vehicle routing problem more difficult to solve. Fortunately, there are optimisation techniques available to handle these situations. In a previous article in the Conversation, I discussed the use of robust optimisation for the railway industry. Similar approaches are applicable for the vehicle routing problem, with only small adjustments. Making it possible to handle the uncertainty in operations of a food bank organisation.
The uncertainty in the vehicle routing problems for food banks make the resulting problems very challenging, but very interesting from a scientific point of view.
Optimisation for food banks
There are a wealth of optimisation problems that arise in food bank organisation. The vehicle routing problem is a classical problem that is a large part of their operations. In addition, food banks mange a large number of paid and volunteer staff. The rostering and scheduling of the staff is another optimisation problem regularly encountered.

